Teaching fractions can be one of the most challenging tasks for any math educator. Fractions often feel abstract and confusing to students, leading to frustration and disengagement. However, after many years of teaching fractions, there are three skills that have transformed how my students understand and work with fractions: decomposing, area models, and benchmark fractions. By incorporating these strategies into my lessons, I’ve seen significant improvement in my students’ fraction comprehension and overall confidence in math. Keep reading to learn the 3 skills that transformed fraction understanding for my students.
Decomposing Fractions
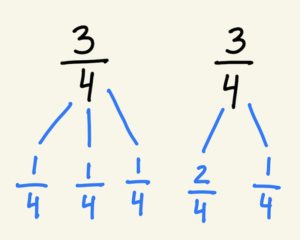
Decomposing fractions involves breaking down a fraction into a sum of smaller fractions with the same denominator. This skill helps students understand the composition of fractions and how they can be manipulated. For instance, when students see that 3/4 can be decomposed into 1/4+1/4+1/4, they start to grasp the concept of fractions as parts of a whole.
To teach decomposing, I use visual aids such as fraction strips and number lines. We work on exercises where students break down fractions into smaller parts and then reassemble them. This hands-on approach allows them to see fractions in a more tangible way, making the abstract concept more concrete.
Decomposing fractions is also incredibly helpful when it comes to mixed numbers. Having students decompose a whole, and understand how much more you need until the next whole, has made converting fractions greater than one into mixed numbers a breeze. It has also helped tremendously when we are subtracting mixed numbers but need to regroup.
Some activities we did to work on this was choral counting, white board decomposing practice, and using word problems that required students to regroup with decomposing or convert into mixed numbers.
Area Models
Area models are a powerful visual tool for teaching fractions. By representing fractions as parts of a shape, usually a rectangle, students can better understand the concept of parts of a whole. Area models also help in teaching equivalent fractions, adding and subtracting fractions, and multiplying fractions.
In my 5th grade classroom, using area models have helped tremendously to understand adding and subtracting fractions. When we find a common denominator to make an equivalent fraction, students were not completely understanding that we were making an equivalent fraction. But when we modeled it with an area model, it was evident that we were not changing how much the fraction is worth, we were just changing the numbers used to represent it. Now, using the algorithm, students have a deeper understanding of what is actually happening. And they would not have had that without. the area models.
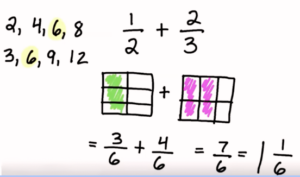
Benchmark Fractions
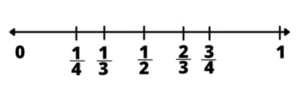
Benchmark fractions, such as 1/4, 1/2, and 3/4, serve as reference points for students. Understanding these benchmarks helps students estimate and compare other fractions more easily. When students can quickly recognize and relate fractions to these common benchmarks, their overall number sense improves.
To incorporate benchmark fractions, we use number lines and real-world examples. I ask students to place different fractions on a number line relative to these benchmarks. In my 5th grade classroom, this helped when we needed to compare fractions. No more tricks of the butterfly method, or creating equivalent fractions to compare. It also helped when we were solving word problems and needed to decide if our answers actually made sense.
Some activities we did to work on this was fraction sorts, where students had to sort equivalent fractions to the benchmark fractions. We also used fraction placemats where students needed to compare the fraction to the benchmark fraction. A few of these resources (and more) are linked at the bottom of this for you to download for free!
The 3 skills that transformed fraction understanding for my students can be incorporated easily! Integrating decomposing fractions, area models, and benchmark fractions into my teaching has revolutionized my students’ understanding of fractions. These skills provide the foundational knowledge and visual tools students need to grasp complex fraction concepts. By making fractions more accessible and less intimidating, I’ve seen my students become more confident and proficient in their math abilities. Want to try incorporating these strategies into your own teaching? Click the link to download: 3 Strategies Resources
Want to learn how I use these in my classroom? Read all about how I use them on my Math Menus.
Want to learn even more about math menus? These courses can help!








One thought on “3 Skills that Transformed Fraction Understanding for My Students”
Hello Julianna,
My name is Akin(ah-keen) Alston. I think you are spot on with your three skills to help students understand fractions. Years ago, my mentor, John Van de Walle told me to spare no effort to build deep conceptual understanding of fractions. Sadly,
fractions are often confusing and not well understood. And knowing algorithms alone isn’t the solution. Fractions stand as a gatekeeper to algebra and all higher mathematics and STEM. I’ll follow you 🤓🤭