When it comes to adding fractions, there are a ton of ways you can do it! I love using the CRA method (concrete, representational, abstract). This post is going to focus on using an area models to add fractions with unlike denominators, which is one of the ways you can complete the representational part. This would be after you have students work with manipulatives, but before they dive into the algorithms surrounding adding fractions.
I love using area models to add fractions with unlike denominators because it is a great branch between fraction tiles and algorithms. Students are able to look at an area model and visually see the connections being made between the two fractions as well as the connections as they find a common denominator.
The first step when given an addition problem with unlike denominators would to be to draw the fractions. I like using area models. Students draw a square. They look at the denominator first. That is how many pieces they need to make. Then they look at the numerator. That is how many pieces they color in.
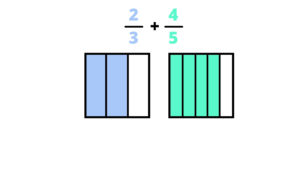
The next step would to be find a common denominator. We do this by listing out the multiples of each denominator until we find something in common. I remind students that the least common denominator will be the easiest to work with (especially when drawing) but any common denominator will work. In this example, 15 is the least common denominator.
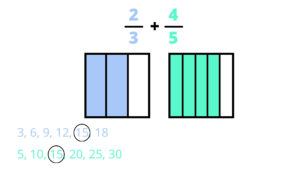
After that, we go back to our original drawings. Since 15 was our common denominator, we need to now make 15 pieces in each. This is easiest when students make their original drawing with vertical lines, and then use horizontal lines at this step. The most important part of this is that students understand that they are not changing the amount that they originally started with. They are just cutting their original into smaller pieces. This is why having a strong understanding of equivalent fractions is so crucial.
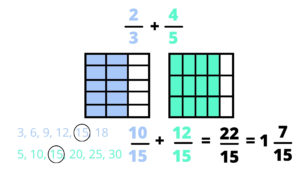
Once they have 15 pieces in each, they use their drawings to find their new equivalent fractions. They count how many are colored in (numerator) and the total number of pieces (denominator) and add them together. From there, you can turn the fraction into a mixed number, if necessary.
This is definitely not the only way to add fractions. But this method tends to allow students to make connections in a way that some other methods do not. Stay tuned for more blog posts about fractions! And if you are dying for more right away, subscribe to my email list!








One thought on “Area Models to Add Fractions”