There are so many options when it comes to subtracting mixed numbers. Over the past few years I have noticed that my students have shown the most success when we do subtracting mixed numbers with regrouping. Here are some reasons why:
-It builds on their understanding of regrouping with whole numbers
-It showcases their understanding of 1 whole as a fraction
-It is easily supported with area models
Step 1:
When using an area model, the first step when given a problem with unlike denominators would to be to draw the fractions. Students can make a choice here (which is another reason I love this): they can draw both pieces of the mixed number (the whole and the fraction) or they can just draw the fraction and use a number to represent the whole. Both strategies work. The only thing is, if you have a large whole number, it could take a while to draw it all. In my example, I decided to just draw the fraction and write the whole number beside it.
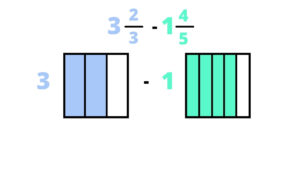
Step 2:
The next step would to be find a common denominator. We do this by listing out the multiples of each denominator until we find something in common. I remind students that the least common denominator will be the easiest to work with (especially when drawing) but any common denominator will work. In this example, 15 is the least common denominator.
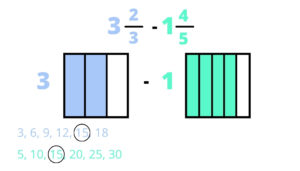
Step 3:
After that, we go back to our original drawings. Since 15 was our common denominator, we need to now make 15 pieces in each. This is easiest when students make their original drawing with vertical lines, and then use horizontal lines at this step. Like last time: the most important part of this is that students understand that they are not changing the amount that they originally started with. They are just cutting their original into smaller pieces. This is why having a strong understanding of equivalent fractions is so crucial.
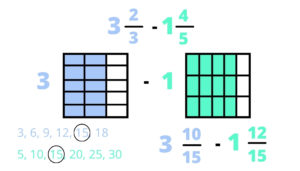
Step 4:
Once they have 15 pieces in each, they use their drawings to find their new equivalent fractions. They count how many are colored in (numerator) and the total number of pieces (denominator). Now they have their equivalent expression to solve. But wait…look at what we have. What do you notice?
This is where students struggle the most…what do I do if I can’t do 10/15 – 12/15? Immediate “uh oh” face appears. What do i do?!?!? Do I need to go back and draw the whole thing? I can’t do this!
But I can…I regroup!
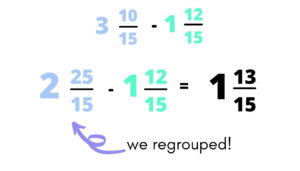
I love this method because it really forces students to use their knowledge of fractions. Knowing that 15/15 is equal to 1 whole, so 3 and 10/15 is the same as 2 and 25/15. If students are having a hard time seeing this, they can even line their problem up vertically so that the regrouping looks similar to what it does when regrouping with whole numbers. Here is what that can look like!
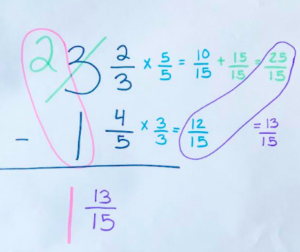
Eventually, students will not be needing to use an area model, so writing it vertically will also come more natural. It is all a process, but a process that we stick with and emphasize so that students get the best possible experience with fractions! This method for subtracting mixed numbers with regrouping builds on a lot of really important fraction number sense concepts, so it is a win all around!
